一道初中奥数题的蒙特卡洛解法
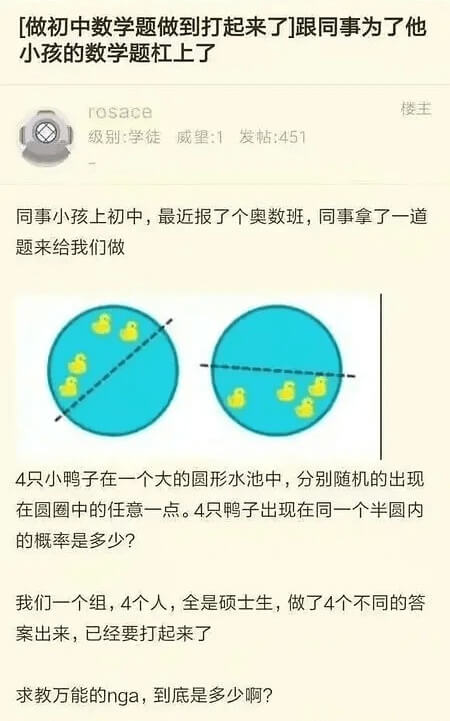
四只鸭子在一个圆形水池中随机游动。某一时刻,四只鸭子在同一半圆内的概率是多少?
这个问题必须隐含一个前提:当水池被分为两半后,任意一只鸭子,要么属于这一边,要么属于另一边,不存在同时属于两边或不属于任何一边的情况。可以把鸭子视作质点,如果鸭子正好落在分割线上,则认为此鸭子属于顺时针方向的一侧。
用极坐标来表示四只鸭子的位置。坐标系的原点是水池圆心,鸭子的坐标为 (ρ, θ),其中 ρ 是极径,即鸭子到原点的距离;θ 是极角,即圆心和鸭子的连线与 x 轴的夹角。
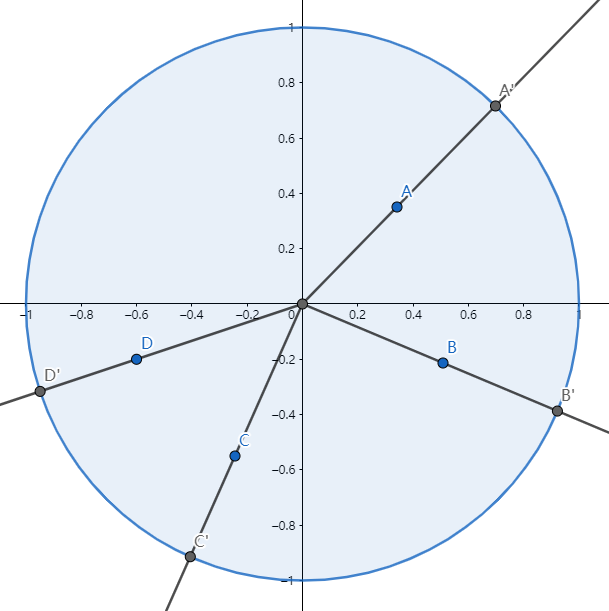
A、B、C、D 四个点表示四只鸭子的位置
观察上图可以发现:鸭子落在半圆的哪一侧仅和极角 θ 有关,和极径 ρ 无关。分别作圆心到 A、B、C、D 四个点的连线,使其连线的延长线和圆周相交,得到四个交点,分别为:A’、B’、C’、D’。问题可以简化为:圆周上随机分布的四个点落在同一侧半圆内的几率有多大。
接下来,用蒙特卡罗方法,编写一段 Python 代码来模拟结果。为了编程方便,将上面的问题转换成另一个等价的问题:在数轴 [0, 1) 的区间内随机分布四个数值,求满足下面任一条件的概率:
- 最大值 - 最小值 < 0.5
- 任意相邻两点的距离 > 0.5
蒙特卡罗方法(Monte Carlo method),也称统计模拟方法,指使用(伪)随机数来解决很多计算问题的方法。
Python 代码如下:
pythonimport random
REPEAT_TIMES = 1000000 # 模拟 100 万次
hits = 0
for i in range(0, REPEAT_TIMES):
points = [
random.random(),
random.random(),
random.random(),
random.random(),
]
points.sort()
if (points[3] - points[0] < 0.5) or \
(points[1] - points[0] > 0.5) or \
(points[2] - points[1] > 0.5) or \
(points[3] - points[2] > 0.5):
hits = hits + 1
print(hits / REPEAT_TIMES)运行 5 遍程序,得到的结果分别是:
- 0.499647
- 0.500212
- 0.49988
- 0.500536
- 0.500006
模拟结果显示答案应该为 0.5。
此外,对于 n 只鸭子,此题的一般解为:n/2(n-1)。

最后附上题目的解题思路
Python 代码如下:
pythonimport random
import math
hits = 0
repeat_times = int(input('输入模拟次数:'))
num_ducks = int(input('输入鸭子数量:'))
def to_fraction(decimal):
'''
尝试将小数化作分数
'''
for denominator in range(2, 256):
numerator = decimal * denominator
numerator_floor = math.floor(numerator)
if numerator - numerator_floor < 0.1 and int(numerator_floor) > 0:
return '{0}/{1}'.format(int(numerator_floor), denominator)
numerator_ceil = math.ceil(numerator)
if numerator_ceil - numerator < 0.1:
return '{0}/{1}'.format(int(numerator_ceil), denominator)
return decimal
for i in range(0, repeat_times):
points = [random.random() for j in range(0, num_ducks)]
points.sort()
for k in range(0, num_ducks):
if points[k] - points[k - 1] > (-0.5 if k == 0 else 0.5):
hits = hits + 1
break
print('鸭子在同一半圆的概率为:{0}'.format(to_fraction(hits / repeat_times)))