Python 的 MRO 和 C3 线性化
MRO,即 Method Resolution Order、方法解析顺序,是 Python 对象调用父类方法时的遍历顺序。由于 Python 支持多重继承,类的继承关系可视作一个有向无环图,方法解析顺序就相当于拓扑排序——将图中节点线性排列。自 Python 2.3 起,新式类通过 C3 线性化算法来计算 MRO。
之所以被称作 C3,是因为算法符合如下三个特性(Consistent with 3 properties):
- 一致性扩展的优先图(a consistent extended precedence graph);
- 保持本地优先顺序(preservation of local precedence order);
- 符合单调性原则(fitting a monotonicity criterion)。
对 Python 而言,如果新式类定义的继承关系无法满足以上三个条件,则会报 TypeError 错误。这三个特性的定义有些拗口。通俗地讲,MRO 列表满足三条规则:
- 如果 A 类的子类总是出现在 B 类的子类之前,则 A 应出现在 B 类之前;
- 当一个类继承了多个父类,则按照定义的先后顺序排列;
- 一个类总是排在其任意一个父类之前。
假设有如下代码:
PYTHONclass A: pass
class A1(A): pass
class A2(A1): pass
class B: pass
class B1(B): pass
class B2(B1): pass
class C(A2, B2): pass
C.mro()得到的结果为:
[<class '__main__.C'>, <class '__main__.A2'>, <class '__main__.A1'>, <class '__main__.A'>, <class '__main__.B2'>, <class '__main__.B1'>, <class '__main__.B'>, <class 'object'>]观察 MRO 可以发现:A 的子类 A1、A2 都排在 B 的子类 B1、B2 之前,所以 A 也排在 B 之前,满足第一条规则;C 继承了 A2 和 B2,在 C 的定义里,A2 排在 B2 之前,所以在 MRO 中,A2 也排在 B2 之前,满足第二条规则。
再来看如下代码:
PYTHONclass A: pass
class B(A): pass
class C(A, B): pass在定义 C 时会报错:
TypeError: Cannot create a consistent method resolution
order (MRO) for bases A, B由于 A 是 B 的父类,按照第三条规则,B 必须排在 A 之前;又按照第二条规则,根据 C 的定义,A 必须排在 B 之前,两条规则产生冲突。如果要让 C 继承 A 和 B,则 C 必须定义为:
PYTHONclass C(B, A): pass此处以维基百科中的例子说明 C3 的具体算法。有如下代码:
PYTHONclass A: pass
class B: pass
class C: pass
class D: pass
class E: pass
class K1(A, B, C): pass
class K2(D, B, E): pass
class K3(D, A): pass
class Z(K1, K2, K3): pass
Z.mro()得到 Z 的 MRO 为:
[<class '__main__.Z'>, <class '__main__.K1'>, <class '__main__.K2'>, <class '__main__.K3'>, <class '__main__.D'>, <class '__main__.A'>, <class '__main__.B'>, <class '__main__.C'>, <class '__main__.E'>, <class 'object'>]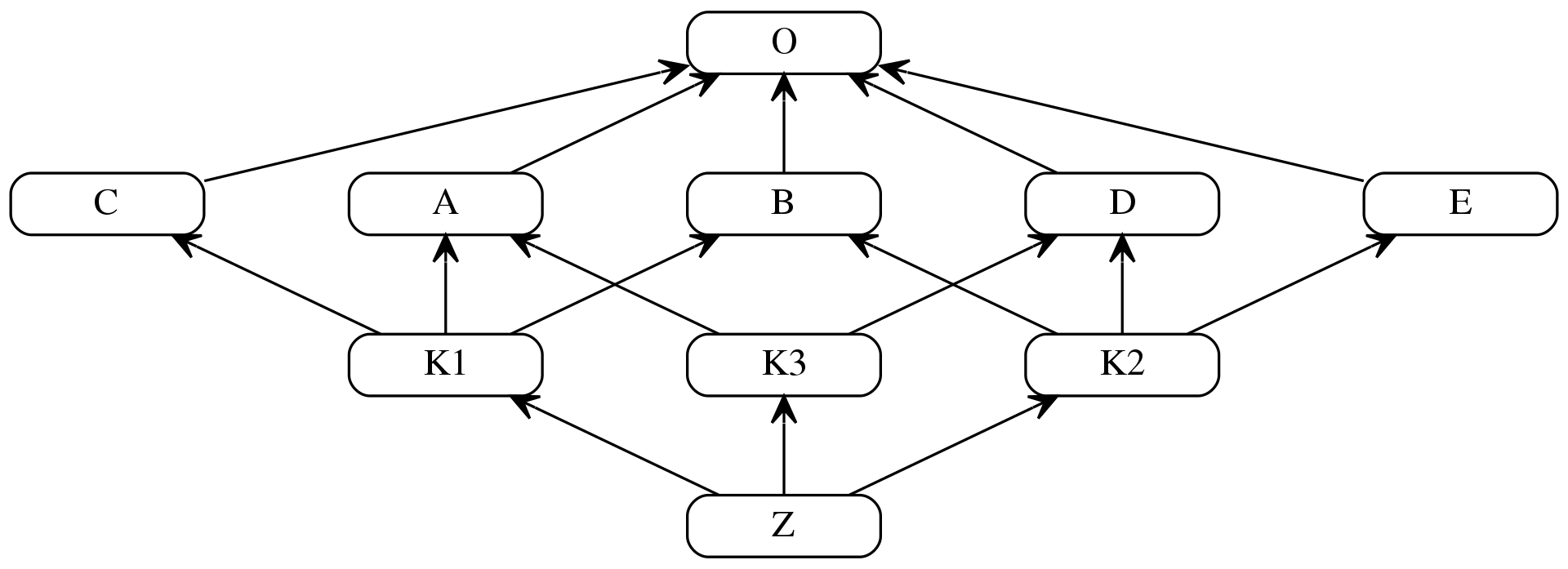
继承关系图(图中 O 相当于 object 类)
计算步骤如下:
L(O) := [O] // O的线性化就是平凡的单例列表[O],因为O没有父类
L(A) := [A] + merge(L(O), [O]) // A的线性化是A加上它的父类的线性化与父类列表的归并
= [A] + merge([O], [O])
= [A, O] // 其结果是简单的将A前置于它的单一父类的线性化
L(B) := [B, O] // B、C、D和E的线性化的计算类似于A
L(C) := [C, O]
L(D) := [D, O]
L(E) := [E, O]
L(K1) := [K1] + merge(L(A), L(B), L(C), [A, B, C]) // 首先找到K1的父类的线性化L(A)、L(B)和L(C),接着将它们归并于父类列表[A, B, C]
= [K1] + merge([A, O], [B, O], [C, O], [A, B, C]) // 类A是第一个归并步骤的良好候选者,因为它只出现为第一个和最后一个列表的头部元素。
= [K1, A] + merge([O], [B, O], [C, O], [B, C]) // 类O不是第二个归并步骤的良好候选者,因为它还出现在列表2和列表3的尾部中;但是类B是良好候选者
= [K1, A, B] + merge([O], [O], [C, O], [C]) // 类C是良好候选者;类O仍出现在列表3的尾部中
= [K1, A, B, C] + merge([O], [O], [O]) // 最后,类O是有效候选者,这还竭尽了所有余下的列表
= [K1, A, B, C, O]
L(K2) := [K2] + merge(L(D), L(B), L(E), [D, B, E])
= [K2] + merge([D, O], [B, O], [E, O], [D, B, E]) // 选择D
= [K2, D] + merge([O], [B, O], [E, O], [B, E]) // 不选O,选择B
= [K2, D, B] + merge([O], [O], [E, O], [E]) // 不选O,选择E
= [K2, D, B, E] + merge([O], [O], [O]) // 选择O
= [K2, D, B, E, O]
L(K3) := [K3] + merge(L(D), L(A), [D, A])
= [K3] + merge([D, O], [A, O], [D, A]) // 选择D
= [K3, D] + merge([O], [A, O], [A]) // 不选O,选择A
= [K3, D, A] + merge([O], [O]) // 选择O
= [K3, D, A, O]
L(Z) := [Z] + merge(L(K1), L(K2), L(K3), [K1, K2, K3])
= [Z] + merge([K1, A, B, C, O], [K2, D, B, E, O], [K3, D, A, O], [K1, K2, K3]) // 选择K1
= [Z, K1] + merge([A, B, C, O], [K2, D, B, E, O], [K3, D, A, O], [K2, K3]) // 不选A,选择K2
= [Z, K1, K2] + merge([A, B, C, O], [D, B, E, O], [K3, D, A, O], [K3]) // 不选A,不选D,选择K3
= [Z, K1, K2, K3] + merge([A, B, C, O], [D, B, E, O], [D, A, O]) // 不选A,选择D
= [Z, K1, K2, K3, D] + merge([A, B, C, O], [B, E, O], [A, O]) // 选择A
= [Z, K1, K2, K3, D, A] + merge([B, C, O], [B, E, O], [O]) // 选择B
= [Z, K1, K2, K3, D, A, B] + merge([C, O], [E, O], [O]) // 选择C
= [Z, K1, K2, K3, D, A, B, C] + merge([O], [E, O], [O]) // 不选O,选择E
= [Z, K1, K2, K3, D, A, B, C, E] + merge([O], [O], [O]) // 选择O
= [Z, K1, K2, K3, D, A, B, C, E, O] // 完成说明一下计算中的各种符号的含义:
[A, B, C, D]表示一个 MRO 列表,其中元素为类名,其顺序为 A、B、C、D;L(Z)表示类 Z 的 MRO 列表;+表示将类名添加到 MRO 列表末尾;merge()可以视作一个生成器,输入多个 MRO 列表,每经过一步计算输出一个类名。
以类 Z 为例,计算 L(Z) 的公式如下:
L(Z) := [Z] + merge(L(K1), L(K2), L(K3), [K1, K2, K3])其中 K1、K2、K3 是 Z 的父类,且按照定义顺序排列。将 L(K1)、L(K2)、L(K3) 展开后得到:
L(Z) := [Z] + merge([K1, A, B, C, O], [K2, D, B, E, O], [K3, D, A, O], [K1, K2, K3])merge() 每一次输出的计算方式如下:
- 选取输入列表中第一个列表作为当前列表;
- 选取当前列表的第一个元素;
- 判断该元素是否为输入的其他 MRO 列表的尾部,即该元素是否出现在其他列表中,且又不为那个列表第一个元素:
- 如果是,选取下一个列表作为当前列表,并重复步骤 2,如果已经遍历了所有列表,则说明不存在有效 MRO;
- 如果否,则输出该元素,并将该元素从所在的每个列表中删除。
- 删除空列表,如果所有列表清空,则结束输出。
比如:
merge([K1, A, B, C, O], [K2, D, B, E, O], [K3, D, A, O], [K1, K2, K3])选取第一个列表 [K1, A, B, C, O] 的第一个元素 K1,该元素出现在最后一个列表 [K1, K2, K3] 中,但是出现位置是该列表的第一个元素,不在尾部,所以输出 K1,并将 K1 从所有列表中移除,得到下一步的计算状态:
merge([A, B, C, O], [K2, D, B, E, O], [K3, D, A, O], [K2, K3])现在,第一个列表的第一个元素是 A,但是该元素出现在第三个列表 [K3, D, A, O] 的尾部(只要出现位置不是第一,即为尾部),所以继续选取下一个列表 [K2, D, B, E, O] 的第一个元素 K2。该元素没有出现在其他列表的尾部,输出该元素,并将其从所有列表中移除,得到下一步的计算状态:
merge([A, B, C, O], [D, B, E, O], [K3, D, A, O], [K3])如此往复,直至所有列表被清空,结束输出,即可获得 Z 的完整 MRO 列表。
这里写得比较啰嗦,主要是因为其他中文作者的文章都写得含糊其辞。